Skip to contents

Gaussian location-scale regression

Source: R/lmls.R
lmls.Rd

The location-scale regression model assumes a normally distributed response variable with one linear predictor for the mean (= the location) and one for the standard deviation (= the scale). The standard deviation is mapped to the linear predictor through a log link.

This function sets up the model object and estimates it with maximum likelihood.

Usage

lmls(
  location,
  scale = ~1,
  data = environment(location),
  light = TRUE,
  maxit = 100,
  reltol = sqrt(.Machine$double.eps)
)

Arguments

location

A two-sided formula with the response variable on the LHS and the predictor for the mean on the RHS.

scale

A one-sided formula with the predictor for the standard deviation on the RHS.

data

A data frame (or list or environment) in which to evaluate the location and scale formulas.

light

If TRUE, the design matrices are removed from the estimated model to save some memory.

maxit

The maximum number of iterations of the Fisher scoring algorithm.

reltol

The relative convergence tolerance of the Fisher scoring algorithm.

Value

A fitted linear model for location and scale as an lmls S3 object. The object has at least the following entries:

  • y: the response vector

  • nobs: the number of observations

  • df: the degrees of freedom

  • df.residual: the residual degrees of freedom

  • coefficients: the regression coefficients as a list with the names location and scale

  • fitted.values: the fitted values as a list with the names location and scale

  • residuals: the response residuals

  • coefficients: the variance-covariance matrices of the regression coefficients as a list with the names location and scale

  • iterations: the number of iterations the Fisher scoring algorithm took to converge

Examples

library(lmls)
m <- lmls(y ~ poly(x, 2), ~ x, data = abdom)
summary(m)
#> 
#> Call:
#> lmls(location = y ~ poly(x, 2), scale = ~x, data = abdom)
#> 
#> Deviance residuals:
#>      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
#> -3.363000 -0.701400 -0.048870 -0.000149  0.623200  4.066000 
#> 
#> Location coefficients (identity link):
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)  226.734      0.563 402.739  < 2e-16 ***
#> poly(x, 2)1 2160.371     15.228 141.871  < 2e-16 ***
#> poly(x, 2)2  -99.184     12.447  -7.968 1.61e-15 ***
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Scale coefficients (log link):
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept) 1.356462   0.096714   14.03   <2e-16 ***
#> x           0.042291   0.003388   12.48   <2e-16 ***
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Residual degrees of freedom: 605
#> Log-likelihood: -2396.41
#> AIC: 4802.82
#> BIC: 4824.89
#> 
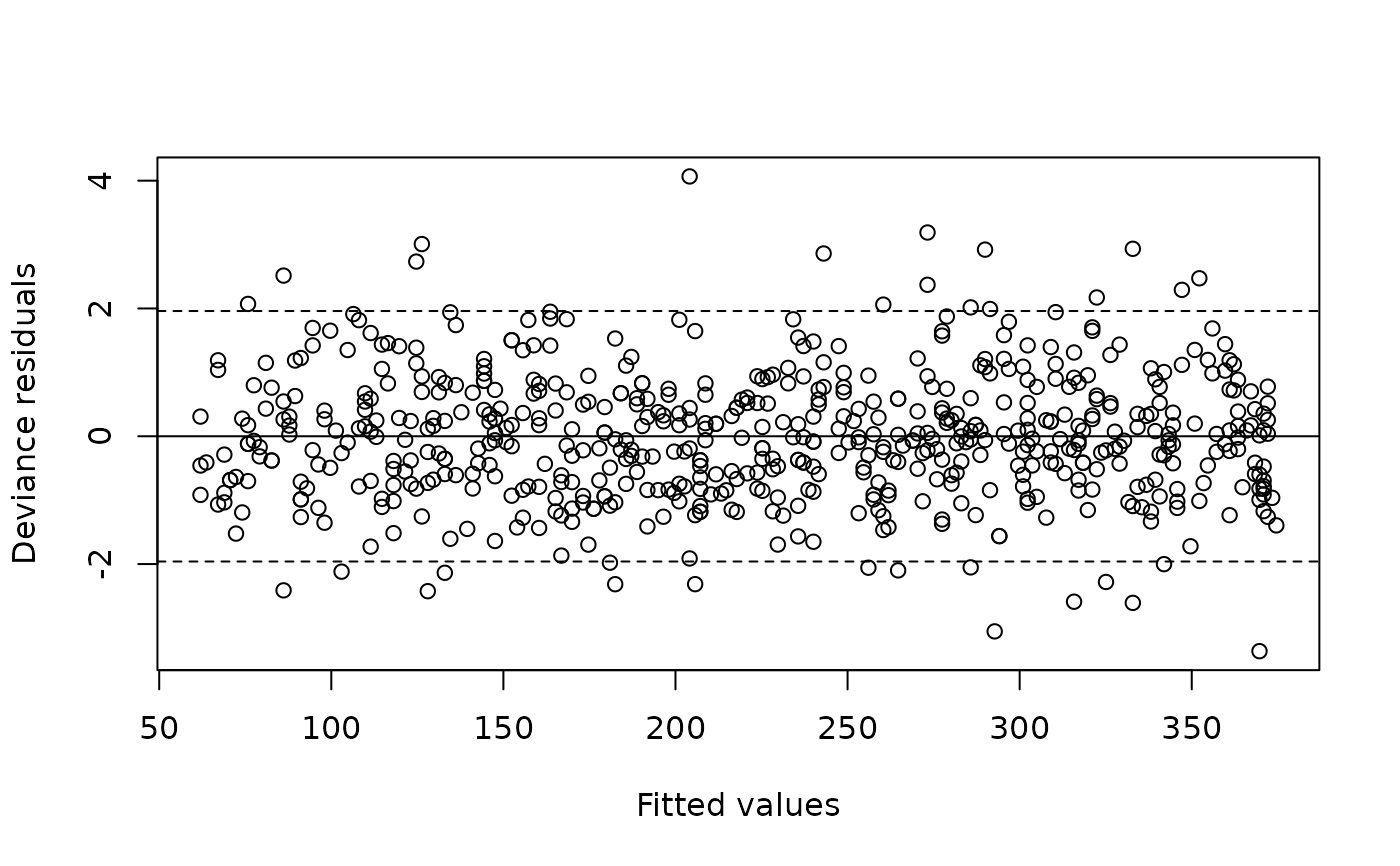
plot(m)

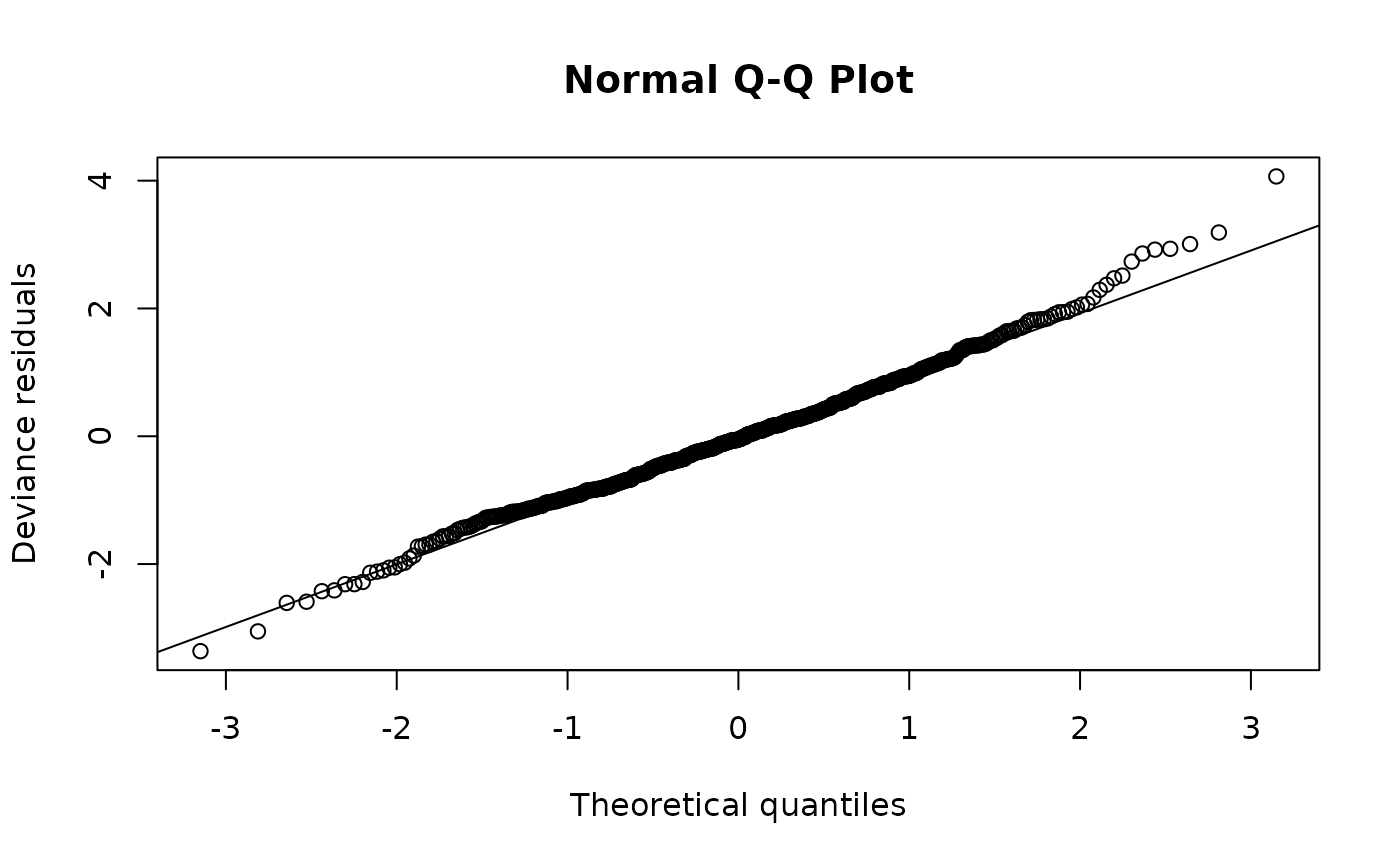
qqnorm(m)